函数 极限 连续
东篱
|
|
736
|
高数

1350 字
|
6 分钟

函数是高数研究的对象，而极限是研究函数的工具，而本章将通过极限这个工具，研究函数的连续性。

函数

课程要点

image-20240115155616524

函数的概念

image-20240115155638255

  • 因为定义域和对应法则有了，值域也就确定了。

下面是一些常用的函数

image-20240115155737487

复合函数

内层函数值域和外层函数定义域的交集不为空才能复合

image-20240115160337684

例题

image-20240117212243862

反函数

image-20240115160736143

  • 单调函数一定有反函数，但是有反函数不一定单调。
  • 有反函数的充要条件是，定义域内任取两个不相等的数，他们所对应y值也一定不相等，即f是定义域到值域的一一映射。

image-20240115162242644

  • 注意，反函数x和y位置互换的两种写法虽然没有问题，但是其图像是不一样的，是关于x=y对称的，详见第三题。

  • 第四题是映射过去又映射回来了，所以答案是x不变。

image-20240115162725473

  • 上面这个例三讲解了如何求反函数，其实就是将x用y表示出来，我们可以发现式子里面有个e的x次方，我们先将e的x次方用y表示出来，剩下的工作就简单了。
  • 具体的解题步骤如下：

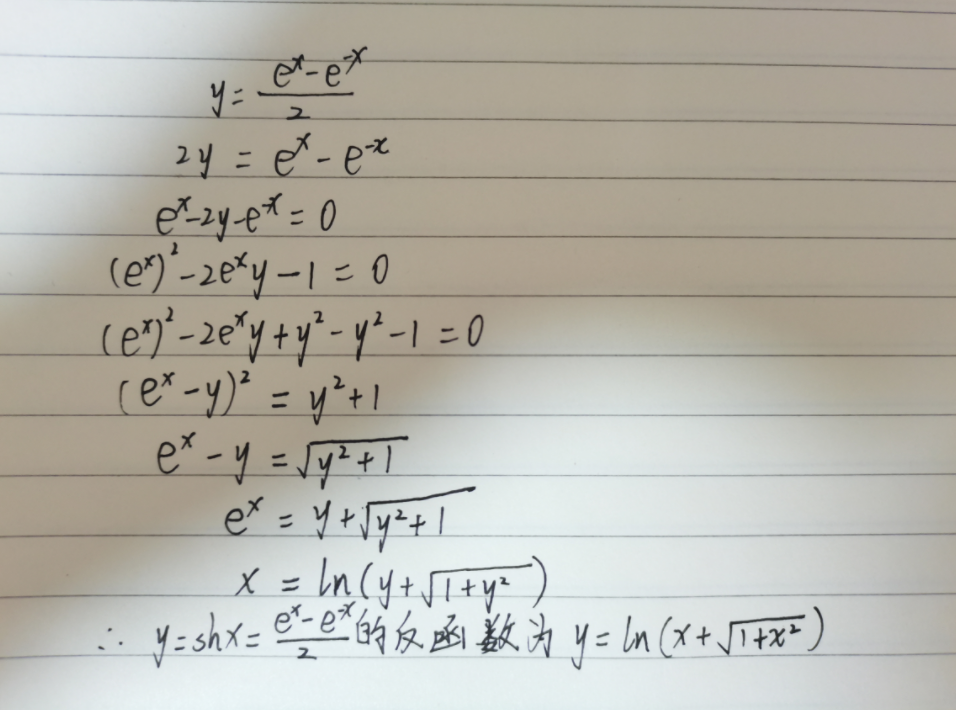
image-20240115164053085

初等函数

image-20240116173310750

Capture_20240116_180048

函数的性质

单调性和奇偶性

image-20240116174404541

Capture_20240116_180131

周期性

image-20240116181810770

有界性

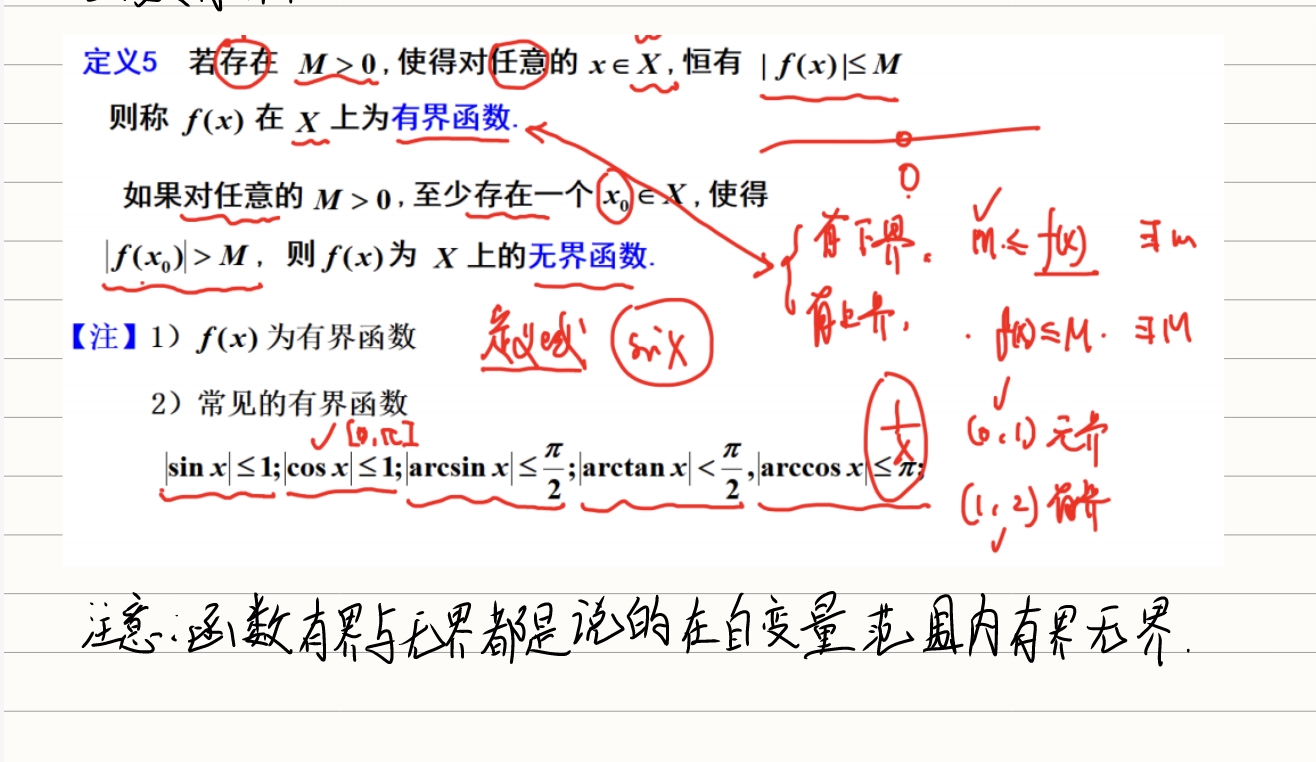
Capture_20240116_183500

Capture_20240117_204000

奇偶性

加法

  • 偶函数+偶函数=偶函数
  • 奇函数+奇函数=奇函数
  • 偶函数+奇函数=非奇非偶函数

乘法

  • 偶函数 × 偶函数 = 偶函数
  • 奇函数 × 奇函数 = 偶函数
  • 偶函数 × 奇函数 = 奇函数

极限

课程要点

image-20240117212522035

image-20240117212938433

数列的极限

概念

微信图片_20240118203410

Capture_20240119_165513

image-20240119170121516

  • 因为该函数奇数列极限=偶数列极限=1，所以原数列极限也等于1

Capture_20240119_172823

常用基本结论

image-20240119173251870

证明：

Capture_20240121_203617

  • 后面很多地方会用到第二条结论，因为取绝对值之后就没有正负号的干扰，进行一些放缩操作就更加容易了。

函数的极限

自变量趋于无穷大

image-20240122162838977

  • 注意，函数极限可以推出数列极限，而数列极限不能推出函数极限（一般可以推特殊，而特殊不能推一般）。
  • 我们有时候求数列极限，就是先求函数极限，然后由此推出数列极限。

Capture_20240122_164947

Capture_20240122_170902

自变量趋于有限值

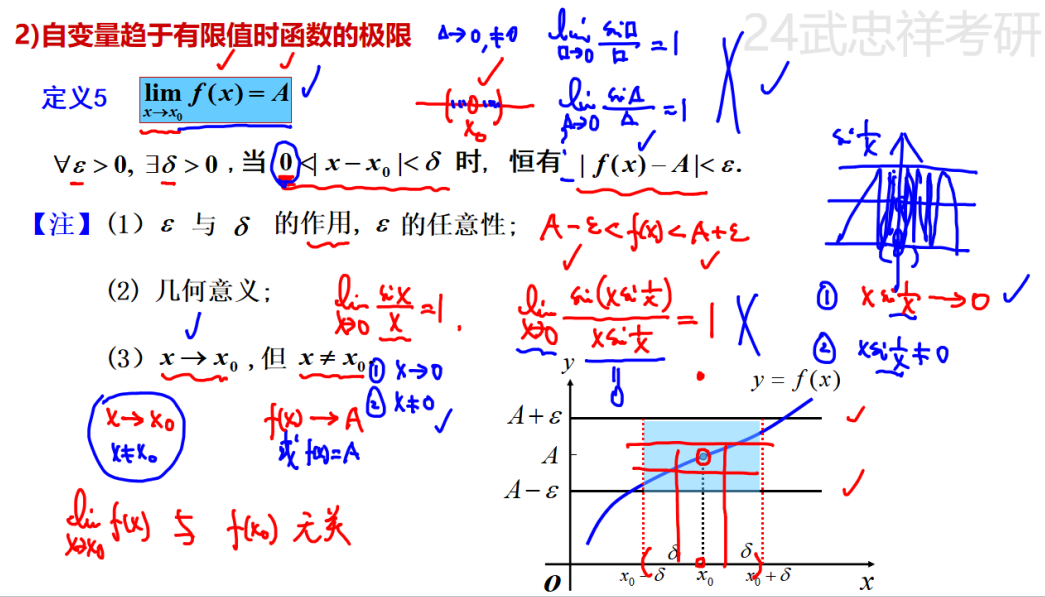
image-20240123191802871

Capture_20240123_191615

左极限与右极限

image-20240124193056261

image-20240124200401375

典型例题

image-20240124201131861

该例子中很明显考察了左右极限问题的第二条，这种一定要分左右极限来单独讨论。

image-20240124202702447

image-20240124202934495

极限的性质

有界性

注意下面这两条反过来都不成立，证明其不成立，举反例即可，我们学习过程中应该积累一些常用的反例。

我单开了一篇文章专门整理反例和常见错误，详见：高数常用反例及经典错误

image-20240125161502710

保号性

  • 极限值的正负保数列项的正负（不带等号）
  • 数列项的正负保极限值的正负（带等号）

不管是数列还是函数，一定要记住，极限值保数列（函数）项不加等号，数列（函数）项保极限值加等号。

image-20240126171716356

Capture_20240126_173149

经典例题

Capture_20240127_210424

也可以用排除法来解这道题，题目中出现一般函数时，我们就可以使用排除法，何为一般函数？其实就是只告诉哦我们 f 满足什么条件，但没有给出 f 的表达式。比如这道题只知道极限等于-1，但是不知道 f 是啥。

换句话说，一般函数就是一般普适情况下的函数，而非某种具体表达式的特殊情况。

那么出现一般函数的情况下我们该如何使用排除法呢？实际上我们需要找一些特殊函数（具体函数），证明三个选项是错的，那么就能找到正确选项了。

image-20240128183505023

极限值与无穷小的关系

image-20240128183830184

注意，三条性质中最重要的是保号性。

极限存在准则

image-20240129185647512

夹逼准则

image-20240129185902977

image-20240129185933293

单调有界准则

Capture_20240130_203923

无穷小量

image-20240131173500900

例题

Capture_20240131_183205

无穷小的性质

image-20240201200518300

无穷大量

概念

image-20240203194410299

常用无穷大量的比较

无穷大量的比较是相当有用的，通过无穷大量的比较，很多题我们根据函数类型就能直接得出结论。

image-20240203201726611

该例题中f，g，h分别为对数，幂，指数，通过无穷大量比较即可得出答案为C。

无穷大量的性质

image-20240204193010357

无穷大量与无界变量的关系

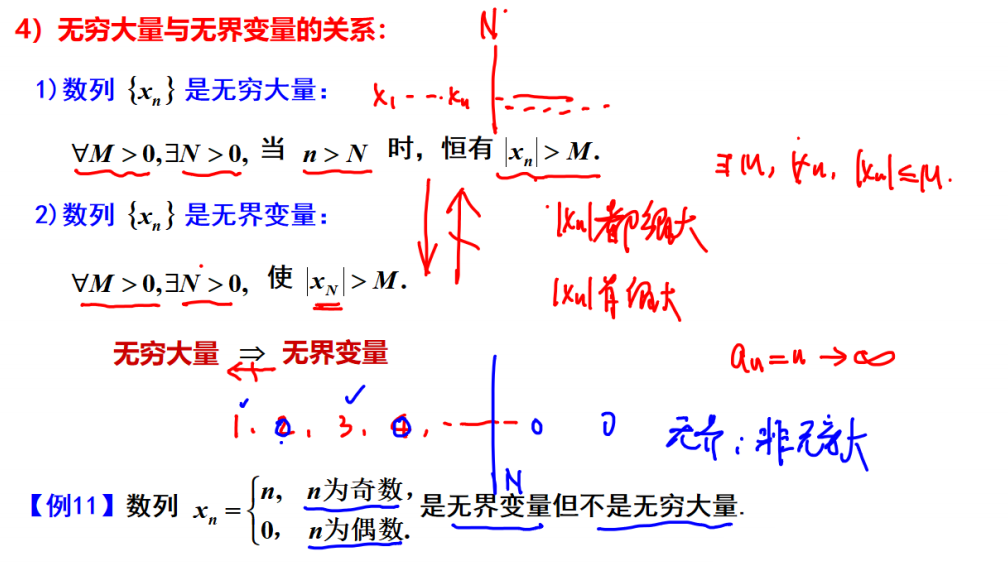
image-20240204193931768

无穷大量与无穷小量的关系

image-20240206205854449

极限内容总结

  • 概念
  • 性质
  • 存在准则
  • 无穷小
  • 无穷大
除特殊说明，博客文章均为东篱原创，依据 CC BY-SA 4.0 许可证进行授权，转载请附上出处链接及本声明。
函数极限考研连续
暂无评论

发送评论 编辑评论 


				

			

						

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
						

					

				

				

					

						

							

								
							

							
							
													

					

				

			

			
			

				

					
				

			

				

											

							
							
						

																					

							
							
						

										
					
											
						

	

		
|´・ω・)ノ
ヾ(≧∇≦*)ゝ
(☆ω☆)
（╯‵□′）╯︵┴─┴
￣﹃￣
(/ω＼)
∠( ᐛ 」∠)＿
(๑•̀ㅁ•́ฅ)
→_→
୧(๑•̀⌄•́๑)૭
٩(ˊᗜˋ*)و
(ノ°ο°)ノ
(´இ皿இ｀)
⌇●﹏●⌇
(ฅ´ω`ฅ)
(╯°A°)╯︵○○○
φ(￣∇￣o)
ヾ(´･ ･｀｡)ノ"
( ง ᵒ̌皿ᵒ̌)ง⁼³₌₃
(ó﹏ò｡)
Σ(っ °Д °;)っ
( ,,´･ω･)ﾉ"(´っω･｀｡)
╮(╯▽╰)╭
o(*////▽////*)q
＞﹏＜
( ๑´•ω•) "(ㆆᴗㆆ)
😂
😀
😅
😊
🙂
🙃
😌
😍
😘
😜
😝
😏
😒
🙄
😳
😡
😔
😫
😱
😭
💩
👻
🙌
🖕
👍
👫
👬
👭
🌚
🌝
🙈
💊
😶
🙏
🍦
🍉
😣
Source: github.com/k4yt3x/flowerhd
	

	

		
颜文字
Emoji
小恐龙
花!
	


									

			

			
			
		

	






上一篇
下一篇 

                    

                    
			        推荐文章
		            

		            

							
数据结构基础

							
							

							
高数常用反例及经典错误

							
							

							
高数学习总纲